一人目，数理音楽．
完全に問題を何にすべきかで路頭に迷っている今日このごろ．
J関数で和音の隣接関係のグラフを書くとどうか，との提案に
素直に作業を進めてきたものの，特別に何かが見つかる様子も見えない．
モードを変えるとdiatonicは五度（7半音）シフトする．
一般のc個中d個ならどうなる，という数学の問題にはできるものの，
音楽的意味へ迫るものでもない．さてさて．
二人目，出会いの数理．
前回一様分布で展開できた話を一般の分布で見てみよう，という回．
やってみると全てが平行に進む．最後の最適行動に関わる解の列が
分布によって変わりうるだけ，とな．
もちろん一様分布に比べて現実問題の分布では比較してどうか，
といった定性的な議論はできる．
まだまだ時はあるし，この後話をどう広げていくかね．
タイミングの数理―最適停止問題 (シリーズ「現代人の数理」)
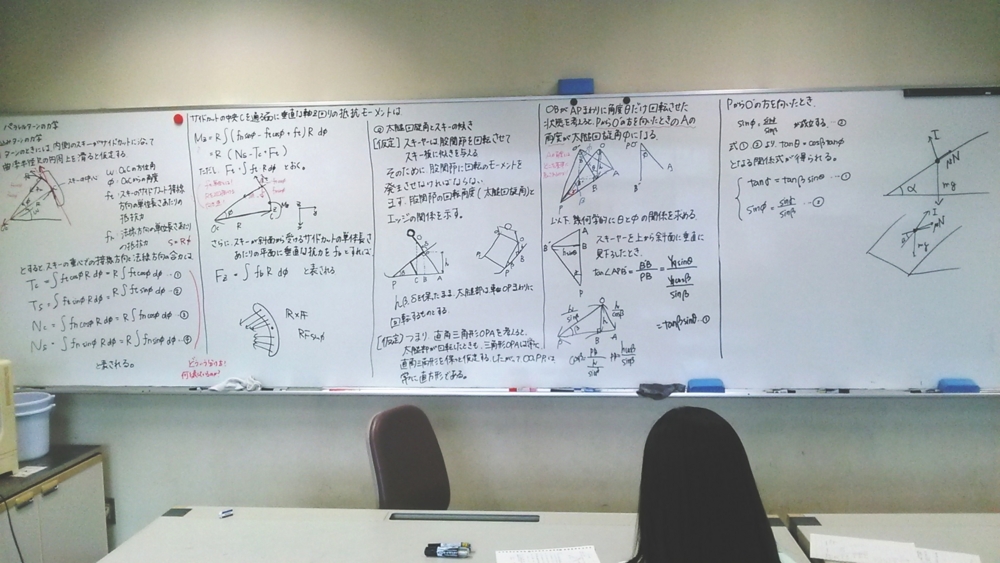
一人目，スキーの力学．
前回は撃力のみの考察によるエッジ角とスキーの回転角度の関係が出ていたのだが，
これを実際に曲線として実現したいなぁ，とボヤーッと思っていた．
が，今日も論文の解読から始まる．しかし色々と不明かつ不安な点があって，途中から頓挫．
こちらも落ち着いて考える時間があれば良いのだが，この所そうもいかない．
何とか自力で形になるものを見つけて欲しいのだが，なかなか．
二人目，最適停止ゲーム．
簡単なカードゲームの最適戦略を検討中．
前回ちょっと参考論文を真似して手を動かして見たら結果らしいものに近づいた．
今日はその詳細を詰めてきてもらった．そしてほとんど解答に近づいたが，
最後の最後，どうも論文が違っているようで修正して，無事着地．
この話の真似をすればもう少し現実のカードゲームに近いモデルが作れそう．
ようやく見えてきたかな．
三人目，数独の数理．
前回は数独の全パターン数を数えたと称する論文を読み始め見てきてもらった．
が，残念なことに全てが数式上で出たわけでなく，肝心な部分はコンピュータによる探索に．
まぁ，予想されたことではあるが，それではこれをどう卒論にしようか．
一方で，当初から頭にある，数独の難しさの定量化を考えるというのも問題としてはあるのだが，
これには数独を解く手順の研究が先決に思える．さて．
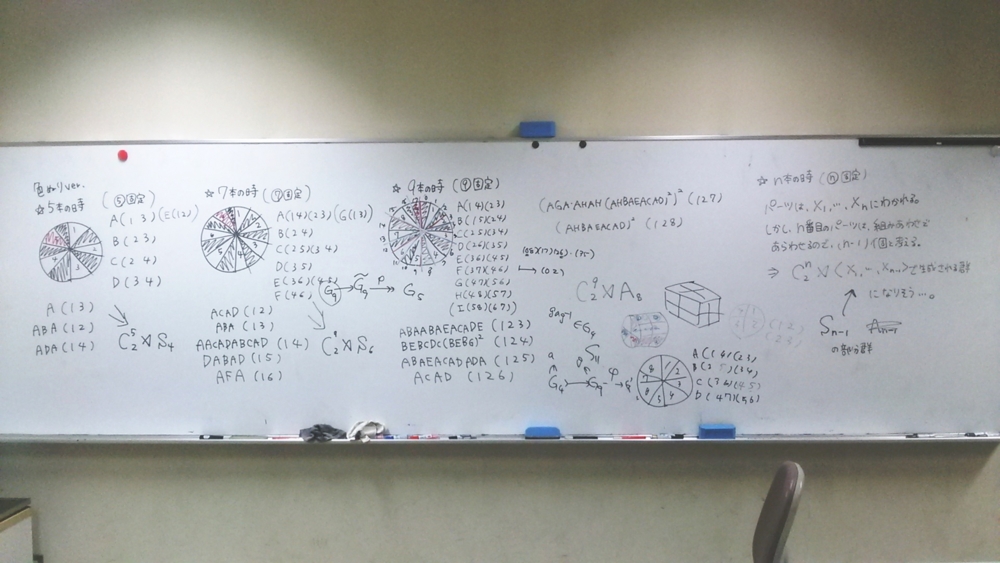
四人目，キューブパズル群．
一進一退を繰り返すこの話．ひたすら置換の計算を力づくで行って群を決定してきたが，
そろそろ別のアプローチがないと，これ以上は進展しない．
前回は同一色で塗りつぶして問題を簡単にする，というアイディアが出た．
ということは塗りつぶす前の群と後の群とでは当然準同型があるわけで，
何らかの群拡大として得るわけにはいかないものだろうか，という提案をしてみた．さて．
群論の味わい ?置換群で解き明かすルービックキューブと15パズル?
で，本日はこの後，３年ゼミ生歓迎会，ってことで露菴へ．
www.good-promise.co.jp
知立呑み，自分は車なので呑まず食に勤しむ．
露菴は一品一品が美味いので飲まなくても楽しめる．
しかし，こうしたイベントがめっきり減ったのも
自分自身にかつての元気さが無くなったことが大きいと感じる今日この頃．
さて，これで後は
年末にかけての猛ダッシュしかありませんね．
一人目，数理音楽．
まずはJ関数でmodeを一つ変えると和音の一音だけが変わることの証明．
結局引き出し論法で示すのが早かった．まぁ，代数的なことだからね．
で，その後やはり何を問題にするのかが問題となる．
それは文化なのか，数理的背景のあることなのか，ということだ．
二人目，出会いの数理．
前回完全情報モデルで一様分布下での最適停止問題に決着を付けた．
今回は分布を変えて考えてごらん，ということで考えてきてもらう．
あらためて整理し直すと，議論の自体は一般の分布で可能．
最適停止のタイミングが変わってくるのだが，
それについての例えば一様分布との比較などができると良い．
本当は絶対ベストを拾う確率が出せると良いのだが，テキストにはそこまで無い．
さて，どうしようかね．
タイミングの数理―最適停止問題 (シリーズ「現代人の数理」)
一人目，スキーの力学．
読んでる論文に詳細が無いということでちょと留まりかけていたのだが，
その前に読んでいたテキストに立ち戻り，質点の運動としての議論だけで，
エッジ角と回転角度と斜面斜度の関係が出せることが改めて分かる．
おぉ，そうするとここから質点の微分方程式を立てても良い．
ようやく核になる話がこれで作れそうだ．
二人目，出会いの数理．
前回，最適方程式を導くに当たり疑問だった漸化式を本日解明．
どうやらちゃんと後退的に計算していけば主張のようになる．
これで一様分布で値が出てくる場合は完全に分かったことになる．
では，より現実味のある分布ではどうか？
というところがオリジナルの研究につながるはずだ．
ところでこの話で，絶対ベストに落ち着く確率は出せていないのだが，
無情報の秘書問題より今回の様に有界な分布が分かっている完全情報のほうが
ベストを選ぶ確率が上がるのだが，考えてみれば確かにそうだね．
タイミングの数理―最適停止問題 (シリーズ「現代人の数理」)
三人目，数独の数理．
こちらものんびりと進めてきたのだが，そろそろ卒論にできる形にせねば．
差し当たり，数独のパターン数をカウントすることを主眼にして進めよう．
実際に議論を行っている論文がPDFで落ちていたのでいくつか紹介．
次回から本格的に見てきてもらうことに．さて，できるかな？
四人目，キューブパズル群．
本来は一般的にどんな群になりそうか検討するために，
具体的な場合での群探しをしていたのが先週，
で，今週その考え方に間違いがあったことに気付いて，一時停滞．
しかし，学生の「同色に塗ってしまって簡単にする」アイディアにより，
ここ３週ばかりの努力が無駄にならずに済む．
さて，それにしても群論的道具が全く登場せずにここまでやってきたのだが，
そろそろ群を準同型の核で捉える方向に進めないかな．
で，気付いたら19:30過ぎていた．疲れた．
群論の味わい ?置換群で解き明かすルービックキューブと15パズル?
一人目，数理音楽．気を抜くと何をしたら良いのかわからなくなるこの分野，
このところはとにかく音楽でよく現れると言われるコード進行図に対し，
数理的モデルを設定して説明する，ということに専念している．
結局，Ｊ表現すると多くの部分は+1,2,3が現れ，トニックの周辺だけ-1,2,3もあるということ．
そして＋の理屈付けとして差し当たり調性の「引力」なるものを想定しよう，ということに．
それは多元的なポテンシャル，とも捉えたい「何か」だ．
でもそろそろ，というよりはここで一度まとめる意味でこれまでのところをTeXにしてもらおう．
J関数についてだけでも，示さねばならないことは多いのだから．
二人目，最適停止ゲーム．
原論文が手にはいらないのだけど，それに近い論文を前回見てもらった．
で，本日はそのやり方を真似てみたわけだが，おや，どうやら上手くいく．
しかし，肝心のその上手くいった部分の写真を撮り忘れていたことに今気づいた．
まぁ，やることは分かっているのだから後は本人の力だけだ．
これが片付いたらもう少しだけポーカーに近い不完全情報ゲームに進めば，
話としてはなかなかイケるのではないかな．
今日は木曜で３年ゼミ日だけど，明日教育実習で大学不在なので振替．
一人目，数独の数理．
前回から数独のパターン数を数える，という話になった．
もちろん肝心な部分は論文に委ねられていてテキストには載っていない．
何でも同値類でどんどん割っていくと，
最終的には４４通りにパターンが集約されるそうなんだが．
ちょいと探すとそれらしい論文が落ちていた．さて，どうするかな．
二人目，数理音楽．
今回は音楽でよく使われるコード進行を集約したような図が
www.readmusicfree.com
ChordSpace Home
にあったりするので，とりあえずその理由を考えてきてもらうことにした．
で，これらの進行をJ-表現でみると，結局±1,2,3の変化だと分かる．
しかしよくよく考えればこれは組合せ的にそうならざるを得ない，とも言える．
ただし方向性があるので，そこはまだ意味を追求できそうなのだ．
何しろ全く手ごろなテキストの無い話だから，すぐに路頭に迷いやすい．
よ～く行先を考えつつ手を付けなければね．
あれ，気付いたら３時間以上やっていた．頭痛い．
三人目，キューブ群．
オリジナルなパズルを考え，その群構造を決定しよう，のコーナー．
ひたすら置換の計算をしてきてもらうことになるのだが，
今日また間違いの発見と，しかしそれによってまたちょっと進む．
ただ，一般のn本切断となるとそろそろ別の道具立てを考えねばキツイかも知れない．
例えば何らかの準同型の核として捉えるやりかたは，
ルービックキューブでもやった方法だ．
できるかな，どうかな？
群論の味わい ?置換群で解き明かすルービックキューブと15パズル?
一人目，スキーの力学．昨日の今日．
モデルづくりのヒントに，と論文を見てきたが，
ここにきて問題の所在を再確認する必要が出てきた．
ターンの前半で十分に板を「踏む」．
そのことによって急斜面でもスピードオーバーにならずにターンが続けられる，
その方法を探ろう，ということだった．
何とかもっと単純なモデルで，しかし本質をつかんだモデルはできないものかなぁ．
ってことで，当初読んでいたテキストに戻ることに．
二人目，最適停止ゲーム．こちらも二日連続で．
問題は色々山積みのままだったので考える事ばかりなのだが，
とりあえず本日は残っていた部分を紹介してもらう．
二人ゲームの最適方程式導出まではこれで大体把握できたわけだが，
当人の考えたいゲームに戻ったとき，
どこまでこの参考にしている論文のやり方が真似できるだろうか．
三人目，数独の数理．こちらは何と４か月ぶりだ．
ラテン方陣をやってきたわけだが，漸く数独に入れるらしい．
本日は数独のパターン数を数える，という課題．ヒューリスティック解を今回は紹介した．
これは Z/10Z での連立方程式の問題になるとも言えるし，
だから数独を解くということは，整数計画問題を解くということになるのだろうね．
でもどこまで当人がやってくれるかは分からない．
とりあえずテキストを読んでいるし，テキストには整数計画法は現れないようだから．
四人目，キューブパズル．さすがに四人目は頭がボーっとするのだが．
オリジナルパズルに手掛け始めたわけだが，
４本カットパズルの群を決定しようとしてひたすら置換の計算をする．
多分A7なんだが，証明に必要な最後のパーツが見つからない．
もう一度落ち着いて整理してきてもらうことに．
で，前回分かったつもりになっていた簡単なキューブパズルの群が間違っている疑惑．
「ピースひとつを固定して考える」方式で二本カット，三本カットも考えてきて，と．
すぐに解決すると思っていたけど，意外と難しい．
群論の味わい ?置換群で解き明かすルービックキューブと15パズル?
一人目，スキーの力学．
なかなか精密な力学モデルが展開されていたと思っていたが，
読んでいたテキスト，肝心なところが省略．
で，それに近い論文を二本ほど検索してあれこれ検討してきてもらうことに．
最後は数値シミュレーションとなってしまうのだけど，
さて，卒論ではどうしていこうかのぅ...
二人目，最適停止ゲーム．
こちらも読んでいるテキストの肝心な部分が省略で，路頭に迷いかける．
こちらも近そうな論文を探して何とか画策中だが，
扱うゲームが微妙に変わっていて，ちょいと悩む．あす，この続き．
三人目，出会いの数理．
こちらは普通にテキストを読んでいるのだが，
意味を考えて理解できる部分と単に数式として見たほうが良い部分とが，
慣れないとなかなか突破しにくい．
こちらも宿題を2,3残したまま次回に持ち越し．
タイミングの数理―最適停止問題 (シリーズ「現代人の数理」)
後期が始まった．一人目，数理音楽．
J表現で基本的な和音が書けることから始まった探索．
数理音楽をやると，いつも何を問題にするかが問題になる．
今回は導音の動きを観察してきたようだが，
組み合わせ的にはそりゃそうだろう，というところまでだった．
voice leading の推力の源を数理的に探す，ってのは魅力的なんだけど，
ともすると何がしたかったのかと自分を見失う．
何か数理的に核になるもの，ないかなぁ...
二人目，出会いの数理．
価値が一様分布に従う場合での最適停止問題．
途中，期待値表現されたある一つの式に引っかかり，延々と議論に．
その式変形を総合的に見ると理解できるのだけど，
こういう書き方するものなのかなぁ...と腑に落ちないまま次回へ．
タイミングの数理―最適停止問題 (シリーズ「現代人の数理」)
キューブパズルの群．もう９月末，申し訳程度に本日．
何しろ当人がすっかり忘れていて，大半の時間を思い出すのに使った．
え，毎回写真だけ取って，ノートにしてなかったの？どゆこと？
ってなわけで，前途多難の後期が始まりそうです．
群論の味わい ?置換群で解き明かすルービックキューブと15パズル?
数理音楽．前回提案したmaximal evenness仮説のもとでの楽曲分析をしてきてもらった．
選んだのは簡単な和音の付けられた「翼をください」（あれ，だったっけ？）にて．
まずはJ-表現で記述することに慣れてもらいながら，
voice leading の推力の源を考えてもらう．考えてもらう，と言っても，
何世紀もかかって音楽家たちの洗練された聴覚によって積み上げられてきたことを
そう容易く説明できるはずもないのだが，
何らかの数理的仕組みをそれでも見出したいわけだ．
さて，音響心理的なバックグラウンド無しで，
どこまで納得の行くものができるだろうか．
最適停止ゲーム．こちらも120日ぶりだ．
ポーカーの数理モデルをさらに単純化した二人ゲームで，
いつまでカードをめくり続けるべきか，という話題．
これは出会いの数理での最適停止問題の二人ゲーム版ともいえる．
参考にしている論文は研究紹介に近いもので，実質的な証明は載っていない．
ということで元論文を探して放浪することになるわけだが，
とりあえず落ちていたPDFで何とかなるかなぁ...
まぁ，ちょっと読んできてもらって考えるとしよう．
一人目，スキーの力学．およそ100日ぶりだ．リハビリを兼ねて復習から．
パラレルターンの力学モデルを作っているところだった．
座標系などなど，段々と過去の記憶が戻ってくる．
読んでいる論文だが，カービングターンと横ずれターンを
素朴なんだがなかなか上手くモデル化しているようだ．
終わり際，結果の式の解釈にえらく戸惑ったが，
力学的意味を考えるより素直に数式を変形すれば良かったわけだ．
さて，当人来週は熊本にボランティアだそうで，偉いじゃないか．
二人目，数理音楽．
調性音楽を公理化したと称する論文を前期は読んでいたが，
どうにもこうにも数学的にすっきりしない．
で，すっかり詰まってしまっていたのだが，
夏の間中ずっと考えていたmaximally evennessを土台にした見方を紹介した．
どこまで調性音楽が説明できるか分からないが，
兎にも角にも具体的な楽曲であれこれ計算してきてもらうこととなった．
何か見つかるかな？
ところで，あと残り３人は全く音沙汰無いなぁ...（と密かに牽制しておく．）
教採も終わって学生も一息つきたいところだろうが，
提出まで150日，動ける人から動いていかないとまた年末に死んでしまう．
で，本日，まず一人が動き始めた，出会いの数理．
数カ月ぶりなので何しろまずは思い出す作業から．
今後の基本となる話をもう一度見直す，という作業をゼミ生本人が企画．
おかげで，こちらもこの話のモードに戻れた，というわけだ．
どういう方針で今後進むか，目標とする研究課題を当人あれこれ考えているようだ．
そういう見通しを持った探求を自らしてくれると助かるなぁ．
さて，この先の話はうまく進むだろうか．
タイミングの数理―最適停止問題 (シリーズ「現代人の数理」)
じゃ～ん．
久しぶりのゼミ飲み（ゼミ生のみ）．
見ての通り，万燈だよ．みんな呑んでるよ（ゼミ生のみ）．
麦ジュースとかカクテルとか熱燗とかみんな呑んでるよ（ゼミ生のみ）．
ってか，平日に設定しないでおくれえぇぇぇー！
まぁ，何だかんだと結局各自の恋沙汰で盛り上がる．
ピーな話とか，ピ～な話とか，ぴ～な話とか．若いねぇ．
それにしても一昔前はほぼ一月に一度何かイベントしていたけど，
この頃は随分と大人しくなったものだね，うちのゼミも．
↑おもむろに熱燗を飲み始める女学生．結局ほぼ一人で徳利二本を空けていた．
その傍らの着ている服の色と変わらない顔の色になった男子学生，後半は沈没．
まずは教採を何とか突破してくれ給え．私の力が発揮できるのはその後だから．
おっと，そうそう，しかるべき理由によってしかるべき歌を贈られ，
その後ワイン半ダースいただいた．
オマケに彼らに軍資金を調達しようとしたら「もう会計は済ませた」と．
なんか申し訳ない．色々申し訳ない．
ボーナス時期だったんだけど，申し訳ない．
今度は教採明け．次こそは飲も．
