スキーの力学，最適停止ゲーム，数独の数理（４年ゼミ）

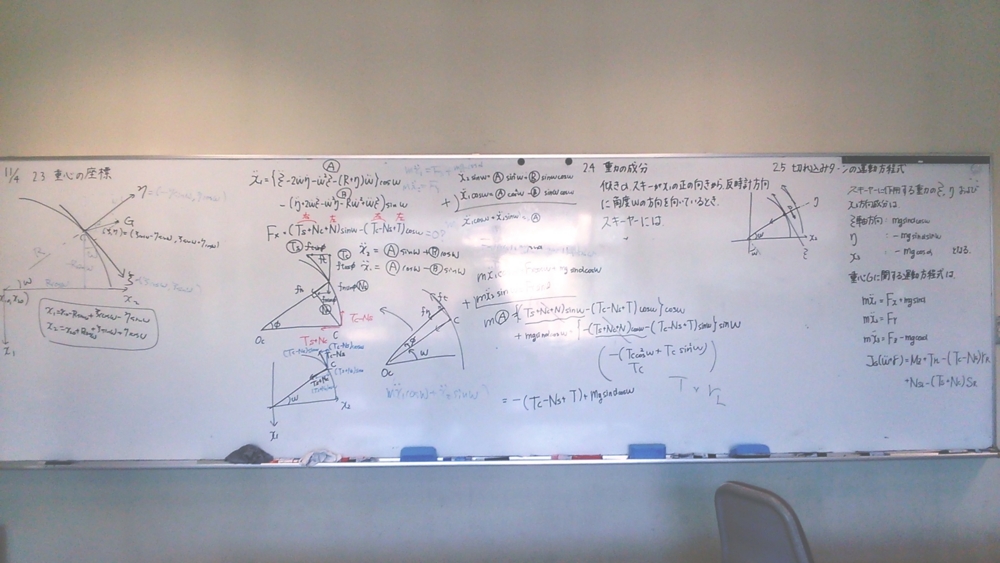
一人目，スキーの力学．
できるだけモデルを簡単にして，核となる微分方程式を見つける作業．
まずは一本スキーにモデルを戻して，連立を解くに必要な微分方程式を作ること．
運動方程式からは３成分，３つが得られる．
そして一本スキーにすると未知数は４つ．あとは回転の運動方程式といったところか．
色々と不安はある．しかし，まずは一つ作り上げねば．

二人目，最適停止ゲーム．
前回ほぼ一枚カードゲームについては決着がついた．
そこでこれからはオリジナルのゲームで話を広げようとしている．
例えば２枚カードゲームで，１枚目の相手のカードは分からない，とすると
かなり通常のカードゲームの形に近くなろう．
しかし情報不完備ゲームとなるわけで，確率変数が一つ増える．
それだけですることは一気に難しかくなるように見えるのだが，さてどうなることか？

三人目，数独の数理．
結局盤面の数え上げも最後は計算機に頼ることになるので，数学的な面白味はない．
もうそういうことであれば，288通りと盤面の数え上げのできる四独全体に作用する
変換群の構造を調べようか，となった．
ここにきてようやくちょっぴり大学の数学っぽくなる．
Burnside Lemmaでどれくらい話が広げられるだろうかね．

「数独」を数学する -世界中を魅了するパズルの奥深い世界-