一人目,立体錯視.
そもそもは,錯視図形のうち,どのような図形が立体化可能か,と検討することだった.
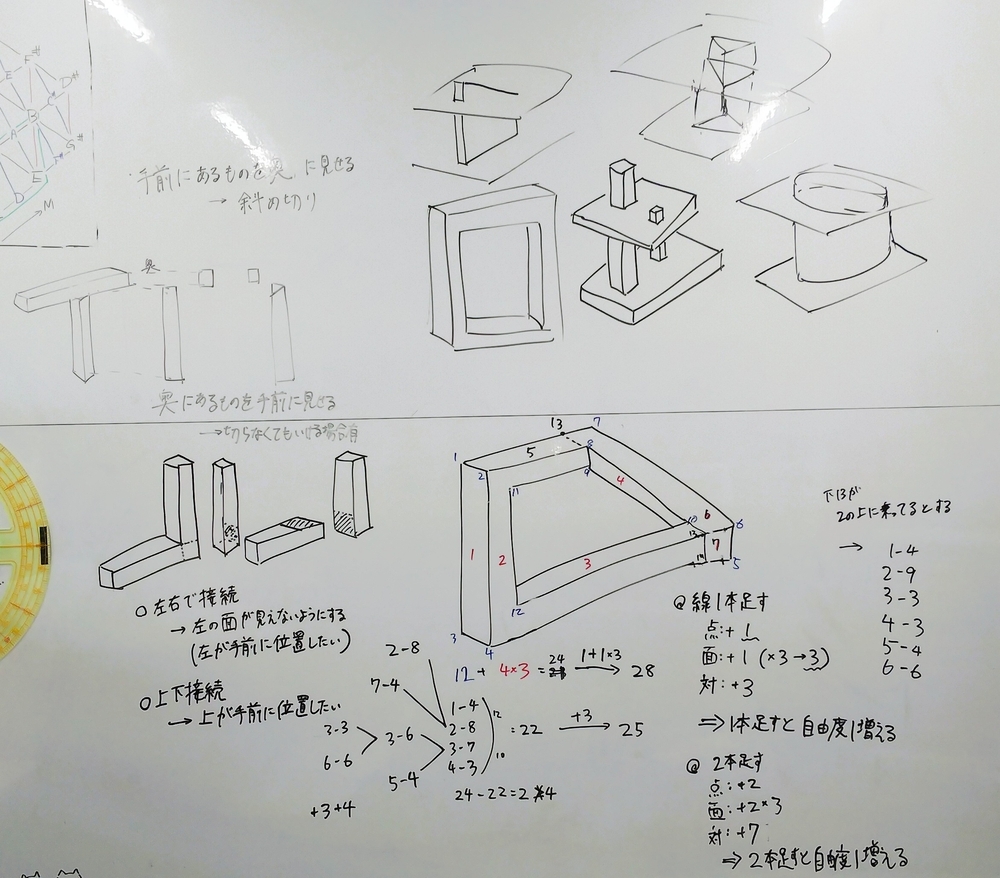
で,その入り口として,再度ペンローズの三角形,四角形を観察する.
切り込み線を入れる/入れないでどのように方程式の自由度が変化するか,それを検討してきてもらう.


二人目,離散体積問題.
エルハート多項式の種々の結果を追っているところ.
でもそろそろオリジナルの内容に進まないとね.

一人目,立体錯視.
そもそもは,錯視図形のうち,どのような図形が立体化可能か,と検討することだった.
で,その入り口として,再度ペンローズの三角形,四角形を観察する.
切り込み線を入れる/入れないでどのように方程式の自由度が変化するか,それを検討してきてもらう.


二人目,離散体積問題.
エルハート多項式の種々の結果を追っているところ.
でもそろそろオリジナルの内容に進まないとね.