スキーの力学，最適停止ゲーム，数独の数理，キューブパズル（４年ゼミ）

本日は已む無き理由により16:30に大学を出ねばならないので，早めにゼミ開始．

一人目，最適停止ゲーム．
元となった論文でどうしても計算が合わなかった部分，どうやら当人が再度計算して
やはり正しかったと確認．そして問題はここから．
２枚カードゲーム版に拡張しようとする際，
どうしてもある種の不等式の安定性が示されねばならない．
しかし際どいところでそれが証明できない．
差し当たり，数値計算で正しいかどうか確認しようということになった．

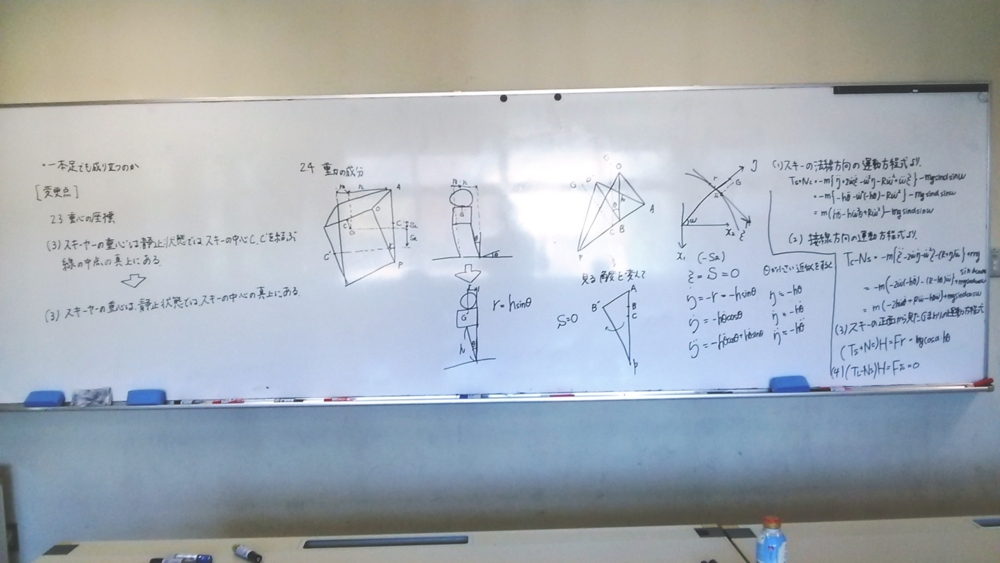
二人目，スキーの力学．
参考論文と逆行して２本足スキーから１本足スキーに戻して力学モデルを構築している．
お蔭でかなりの部分がはっきりしてきた．
あとはまず数値解析を行ってどの程度スキーが再現できているか見るところまで行けそうだ．

三人目，数独の数理．
四独のパターンを四独に作用する群で実際に分類しよう，という試み．
闇雲にパターンを探してもきりがなく，
先にある程度群を確定してから，と行きたいところだ．
幸い，一ブロックを固定すれば全パターンは24．
これならBurnside lemmaを具体的に見せられるだろう．

「数独」を数学する -世界中を魅了するパズルの奥深い世界-

四人目，キューブパズル群．
いつの間にかたくさんの結果が積みあがってそれなりの形になってきた．
本日は卒論の構成見直しに注力．
そうそう，これは図が無いと全く伝わらないので描かねばね．

群論の味わい ?置換群で解き明かすルービックキューブと15パズル?