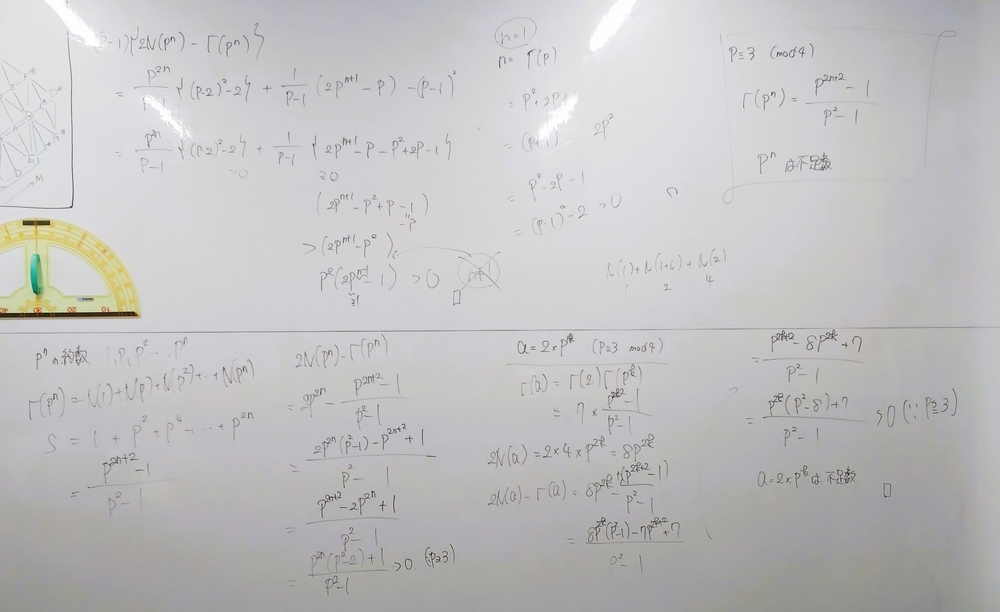2023-10-31

ライツアウトの数理，野球の統計学，倒立振子の制御工学（４年ゼミ）

ゼミ2023年度卒

一人目，ライツアウトの数理．
前回，サイズが偶数の場合で主結果が導かれることを見た．
今回は奇数の場合．キーになるのはFibonacci多項式の関係式 $p_{2n+1}(t)=tp_n(t)^2$ ．
そこで， $\sigma:n\mapsto 2n+1$ を考え， $n=\sigma^b(2s)$ について考えれば，固有多項式 $\Phi_n(\lambda)=p_n(\lambda+1)=(\lambda+1)^{2^b-1}\Phi_{2s}(\lambda)^{2^{b}}$
となるのが分かり，固有値1の重複度が $2^b-1$ ，残りの固有値の重複度が $2\cdot 2^b=2^{b+1}$ となり，すると
$T_n\sim J(1,2^b-1)\oplus J(\alpha_1,2^{b+1})\oplus\cdots\oplus J(\alpha_s,2^{b+1})$
が分かるので， $\mathbb{F}_2$ での特徴であるJordan細胞に関する性質 $J(\alpha,d)^{2^b}=\alpha^d E_d, 2^b\ge d$ が使える形になる．
さて，求めたかったのは ${\rm rank}(p_n(T_n))$ であったが， $p_n(t)=t^{2^b-1}p_{2s}(t)^{2^b}=t^{2^b-1}\nu_{2s}(t)^{2^{b+1}}$ に注意すれば，
$\begin{align*} p_n(T_n)\sim &(J(1,2^b-1)\oplus J(\alpha_1,2^{b+1})\oplus\cdots\oplus J(\alpha_s,2^{b+1}))^{2^b-1}\\ &\cdot \nu_{2s}( (J(1,2^b-1)\oplus J(\alpha_1,2^{b+1})\oplus\cdots\oplus J(\alpha_s,2^{b+1}))^{2^{b+1}} )\\ = &K(1,2^b-1)\oplus K(\alpha_1,2^{b+1})\oplus\cdots\oplus K(\alpha_s,2^{b+1})\\ &\cdot \nu_{2s}(E_{2^b-1}\oplus \alpha_1^{2^{b+1}}E_{2^{b+1}}\oplus\cdots\oplus \alpha_s^{2^{b+1}}E_{2^{b+1}})\\ = &\nu_{2s}(1)K(1,2^b-1)\oplus \nu_{2s}(\alpha_1)^{2^{b+1}}K(\alpha_1,2^{b+1})\oplus\cdots\oplus \nu_{2s}(\alpha_s)^{2^{b+1}}K(\alpha_s,2^{b+1}) \end{align*}$
となる．ただし， $K(\alpha,d)=J(\alpha,d)^{2^b-1}$ と置いた．
結局， ${\rm rank}(T_n)$ を制御するのは $p_n(\alpha)=0$ となる固有値 $\alpha$ の個数であり，前回同様の議論をすれば，
${\rm rank}(T_n)=n-\deg({\rm GCM}(p_n(t),p_n(t+1)))$
が導かれる．
本当は細かい場合分けが必要なところもあるが，大方この方向で証明が完結する．
drive.google.com

二人目，野球の統計．
もう，尻に火がついた状態なので，短期間で実行できそうな話を探すと，DEA（包絡分析法）を使った遊びができそうである．企業価値などを測る一つの方法らしいが，野球に適用したいくつかの先行研究もあって何かできるでしょう，という感じ．
数学的な部分は線形計画法のところのみ，かな．

多変量解析法入門 (ライブラリ新数学大系)

作者:靖, 永田,雅彦, 棟近
サイエンス社

Amazon

三人目，制御理論．こちらも，5/26以来で5ヶ月ぶりの再開．
そして，ネタも定まっていなかったのだが，ひょっこり現れて「倒立振子
の制御」をやるとこのこと．
ネットで探せばそのものズバリのテキストがあって，もう，それを読むことにしよう，となった．

倒立振子で学ぶ制御工学

作者:川田昌克,東俊一,市原裕之,浦久保孝光,大塚敏之,甲斐健也,國松禎明,澤田賢治,永原正章,南裕樹
森北出版

Amazon

2023-10-30

完全数（４年ゼミ）

ゼミ2023年度卒

ノルム完全数の探索．
今回， $p\equiv3\pmod{4}$ 型の奇数のみを因数に持つ数のノルム和の評価を見た．
結論としては，過剰数は無いということ．
$a=p_1^{e_1}p_2^{e_2}\cdots p_n^{e_n}, \quad p_i\equiv3\pmod{4}$
の $Z[i$ ] におけるノルム和 $\Gamma(a)$ と $a$ との比が
$\displaystyle\prod_{i=1}^n\frac{p_i^{2e_i+2}-1}{p_i^2-1}\Big/p_i^{e_i}=\prod_{i=1}^n\frac{1-\frac{1}{p_i^{2e_i}}}{1-\frac{1}{p_i^2}}<\prod_{i=1}^n\frac{1}{1-\frac{1}{p_i^2}}<\zeta(2)=\frac{\pi^2}{6}<2$
となって，不足数になってしまう．
ということで，次は $p\equiv1\pmod{4}$ を触ることになった．

初等整数論講義第2版

作者:高木貞治
共立出版

Amazon

初等整数論 ―数論幾何への誘い― (共立講座数学探検 6)

作者:山崎隆雄
共立出版

Amazon

2023-10-27

結晶群，キューブ群（４年ゼミ）

ゼミ2023年度卒

一人目，キューブ群．
交換子利用の覚えやすい手順による解法の探求．
$X=[U,R$ ,Y=[U^{-1},L^{-1}]] を主に使うやり方では，どうしても2面体の扱いが複雑になりがち．
そこで割り切って，3面体では $X,Y$ によって，2面体は例えば $(RU)^2(UR)^{-2}$ などの2面体だけを動かす操作で揃えることにしたらどうかと提案．

群論の味わい－置換群で解き明かすルービックキューブと15パズル－

作者:David Joyner
共立出版

Amazon

二人目，結晶群．
4次元の正多胞体の数え上げを Burnside による方法で，といきたかったが詰まるようなので，鏡映群による方法が書かれた論文を紹介したら，読んできたらしい．
しばらくはこの方向で粘ってみよう．

文様の幾何学―文様における群作用と対称性

作者:川崎徹郎
牧野書店

Amazon

2023-10-24

ライツアウトの数理，野球の統計学（4年ゼミ）

ゼミ2023年度卒

一人目，ライツアウトの数理．
今回は三重対角行列 $T_d$ の固有多項式を考える．
$\mathbb{F}_2$ での話なので符号を機にする必要がないことに注意すれば，固有多項式 $\Phi_d(\lambda)=\det(T_d+\lambda E_d)$ の計算は，Lights Out行列 $A$ で ${\rm rank}$ を求めた方法と全く同じである．
つまり，行列 $B$ において， $T_d\to \lambda+1,\ E_d\to 1$ と置き換えてやれば，
$\Phi_d(\lambda)=p_d(\lambda+1)$
と求められる．また，このときに行った行基本変形の結果，対角線上に 1 が $d-1$ 個， $p_d(\lambda+1)$ が1個並ぶので，各固有値 $\lambda=\alpha_k$ ごとに，
$\dim(\ker(T_d+\lambda E_d))=1$
となることが分かる．すなわち，各固有値に対する固有空間の次元は1だと分かる．

ところで， $\mathbb{F}_2$ 係数のFibonacci多項式 $p_n(t)$ は， $\nu_0(t)=\nu_1(t)=1$ および漸化式
$\nu_{k+2}(t)=\begin{cases} \nu_{k+1}(t)+\nu_k(t),&\text{ $k$が奇数のとき,}\\ t\nu_{k+1}(t)+\nu_k(t),&\text{ $k$が偶数のとき,} \end{cases}$
によって定められる多項式 $\nu_k(t)$ を用いて，
$p_{k}(t)=\begin{cases} t(\nu_k(t))^2,&\text{ $k$が奇数のとき,}\\ (\nu_k(t))^2,&\text{ $k$が偶数のとき} \end{cases}$
と表されることが示される．更に， $\nu_k(t)=0$ は $\mathbb{F}_2$ の閉包において重解を持たず，分離的であることも示される．したがって偶数 $k=2d$ の場合， $p_{2d}(t)=0$ のすべての解は2重解のみであり， $\Phi_{2d}(\lambda)=p_{2d}(\lambda+1)=0$ の解である $T_{2d}$ の固有値も全て2重解のみとなる．
一方，各固有値の固有空間は1次元だったことと合わせると， $T_{2d}$ のJordan標準形は2次ブロックだけの直和に分解され，
$T_{2d}\sim J(\alpha_1,2)\oplus\cdots \oplus J(\alpha_d,2)$
となることが分かる．

さて以前示したように， $\mathbb{F}_2$ での特有な現象として $2^b\ge d$ ならば
$J(\alpha,d)^{2^b}=\alpha^{2^b}E_d$
となったのであった．すると
$T^2_{2d}\sim \alpha_1^2E_2\oplus\cdots \oplus\alpha_d^2E_2$
となり，つまり，
$\begin{align} p_{2d}(T_{2d})&=\nu_{2d}(T_{2d})^2=\nu_{2d}(T_{2d}^2)\sim \nu_{2d}(\alpha_1^2)E_2\oplus\cdots\oplus\nu_{2d}(\alpha_d^2)E_2\\ &\sim p_{2d}(\alpha_1)E_2\oplus\cdots\oplus p_{2d}(\alpha_d)E_2 \end{align}$
といった対角行列に相似になる．となると，
${\rm rank}(p_{2d}(T_{2d}))=2d-2\#\{\alpha_k\mid p_{2d}(\alpha_k)=0\}$
ということになるが，もともと $\alpha_k$ は固有値，すなわち $\Phi_{2d}(\lambda)=p_{2d}(\lambda+1)=0$ の解でもあったから結局，
$\begin{align} {\rm rank}(p_{2d}(T_{2d}))&=2d-2\#\{\alpha\mid p_{2d}(\alpha)=p_{2d}(\alpha+1)=0\}\\ &=2d-\deg({\rm GCD}(p_{2d}(t),p_{2d}(t+1))) \end{align}$
ということになる．こうして，まず $n=2d$ のLights Out行列 $A$ の ${\rm rank}(A)$ が決定できた．
drive.google.com

二人目，野球の統計学的な何か．
こちらも5/16以来のゼミとなり，5ヶ月以上が過ぎてしまった．
しかも，自分でなにか進めていてくれたわけでもなく，手遅れに近い．
今流行のセイバーメトリクス的な何かをしようとしているようだが，何しろ問題意識が定まっていない．
この状態は，本来9月上旬であるべきで，50日ほど間に合っていない計算になる．さてどうするかね．

多変量解析法入門 (ライブラリ新数学大系)

作者:靖, 永田,雅彦, 棟近
サイエンス社

Amazon

2023-10-23

完全数（４年ゼミ）

ゼミ2023年度卒

完全数探し．なんとこちらは5/26以来で5ヶ月ぶりのゼミ再開である．
ただ偉いのは，自分で探究活動を続けていたこと．
実際，本日のゼミでもこの休み期間中の進捗報告をしてくれたし，LaTeXも順調に書き加えているようだ．
まぁ，これが本来のゼミの姿だよな．

さて，本日の報告は， $Z[i$ ] でのノルム完全数探しと，通常の自然数での奇数の完全数があったとしたら，どんな条件がつくのか，の2本立てで並行して探求している模様．
よくよく振り返ってみると， $Z[i$ ] でのノルム完全数はまだ見つけていなかったらしい．
不等式評価を重ねて不足数・過剰数の条件・範囲を調べているところ．
さて，見つかるのだろうか？

初等整数論講義第2版

作者:高木貞治
共立出版

Amazon

初等整数論 ―数論幾何への誘い― (共立講座数学探検 6)

作者:山崎隆雄
共立出版

Amazon

2023-10-12

結晶群，キューブ群（４年ゼミ）

ゼミ2023年度卒

一人目，キューブ群．検討してきた交換子 $X=[U,R], Y=[U^{-1},L^{-1}]$ による手順の作成の続き．
例えば3面体だけのキューブであれば，これら交換子の特徴を活かして，1面から順に揃えたりしない方法が作れるかもしれない，と試みた．が，かえって手順が増えるし，実際に行うには複雑すぎる，という結果に．
どうやら手順として確立するには，Cayley graphのどのあたりにハブを置いて，覚えるべき手順の数と覚えるべき盤面の数のバランスが重要のようだ．

群論の味わい－置換群で解き明かすルービックキューブと15パズル－

作者:David Joyner
共立出版

Amazon

二人目，結晶群改め， $SO(4)$ の有限部分群の決定をしてみよう．
ところが $SO(3)$ において，幾何学的な直観で誤魔化していた部分が $SO(4)$ ではままならなくなることに行き着き，そこで一旦ブレーキがかかった．

文様の幾何学―文様における群作用と対称性

作者:川崎徹郎
牧野書店

Amazon

2023-10-10

ライツアウトの数理（4年ゼミ）

ゼミ2023年度卒

ライツアウト行列の rank を巡って．
ノイマン近傍型にライトのon/offを切り替えるこのゲームの操作は，Lights Out行列
$A=\begin{pmatrix} T_d&E_d&O_d&O_d&\cdots&O_d\\ E_d&T_d&E_d&O_d&\cdots&O_d\\ O_d&E_d&T_d&E_d&\cdots&O_d\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ O_d&\cdots&E_d&T_d&E_d&O_d\\ O_d&\cdots&O_d&E_d&T_d&E_d\\ O_d&\cdots&O_d&O_d&E_d&T_d \end{pmatrix}$
と表される．求めたいのは ${\rm rank}(A)$ だ．ただし， $T_d$ は $\mathbb{F}_2$ 係数の三重対角行列
$T_d=\begin{pmatrix} 1&1&0&0&\cdots&0\\ 1&1&1&0&\cdots&0\\ 0&1&1&1&\cdots&0\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ 0&\cdots&1&1&1&0\\ 0&\cdots&0&1&1&1\\ 0&\cdots&0&0&1&1 \end{pmatrix},$
$E_d,O_d$ はそれぞれ， $d$ 次単位行列とゼロ行列である．
${\rm rank}(A)$ を求める代わりに，はじめの $d$ 行を最後に移動した，
$B=\begin{pmatrix} E_d&T_d&E_d&O_d&\cdots&O_d\\ O_d&E_d&T_d&E_d&\cdots&O_d\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ O_d&\cdots&E_d&T_d&E_d&O_d\\ O_d&\cdots&O_d&E_d&T_d&E_d\\ O_d&\cdots&O_d&O_d&E_d&T_d\\ T_d&E_d&O_d&O_d&\cdots&O_d\\ \end{pmatrix}$
の rank を求めるほうが容易い．このその最下段を頭から順に消去していくわけだが，はじめの $d$ 行とラストの $d$ 行とで，
$\begin{pmatrix} E_d&T_d&E_d&O_d&\cdots\\ T_d&E_d&O_d&O_d&\cdots \end{pmatrix} \to \begin{pmatrix} E_d&T_d&E_d&O_d&\cdots\\ O_d&T_d^2+E_d&T_d&O_d&\cdots \end{pmatrix}$
と行基本変形でき，これを繰り返せば $(k+1)$ stepで
$\begin{pmatrix} \cdots&E_d&T_d&E_d&\cdots\\ \cdots&P_k&Q_k&O_d&\cdots \end{pmatrix} \to \begin{pmatrix} \cdots&E_d&T_d&E_d&\cdots\\ \cdots&O_d&P_{k+1}=T_dP_k+Q_k&Q_{k+1}=P_k&\cdots \end{pmatrix}$
と変形される．こうしてFibonacci多項式の漸化式
$\begin{pmatrix}P_{k+1}\\Q_{k+1}\end{pmatrix} =\begin{pmatrix}T_d&E_d\\E_d&O_d\end{pmatrix} \begin{pmatrix}P_{k}\\Q_{k}\end{pmatrix}$
が登場し，特に最後のステップによってラスト $d$ 行は
$\begin{pmatrix} O_d&\cdots&P_{d}=p_d(T_d)\end{pmatrix}$
と， Fibonacci多項式 $p_d(t)$ を用いて表示される．こうして，
${\rm rank}(A)={\rm rank}(B)=d(d-1)+{\rm rank}(p_d(T_d))$
となる所まで来た．次にすべきは， ${\rm rank}(p_d(T_d))$ を求めることであるが，今度は三重対角行列 $T_d$ の固有多項式が関わってくることになる．
okiraku-semi.hatenablog.jp

drive.google.com

2023-10-06

結晶群（４年ゼミ）

ゼミ2023年度卒

結晶群．残っていた，正20面体群の決定まで終了．
さて，この先どうするか，ということになったが，結晶群ではなく，高次元の正胞体を数える方向でやってみることになった．
とりあえず， $SO(3)$ の有限部分群の決定方法を参考に， $SO(4)$ で同じことをやってみる．
答えは世間的にはよく知られているけれど，どうなるかな．

文様の幾何学―文様における群作用と対称性

作者:川崎徹郎
牧野書店

Amazon

2023-10-04

キューブ群（４年ゼミ）

ゼミ2023年度卒

キューブ群．オリジナルの手順を見つける話の続き．
交換子 $X=[U,R], Y=[U^{-1},L^{-1}]$ （と少量の基本操作）の組み合わせで手順を構成する話には，ひとしきり出来上がった．ただ，手数が多すぎ．この先は，手数を減らす方法を考えたい．例えば，現行は完全一面から始めて下から順にすでにできた部分が壊れないように残りの面を何とかして完成させようとしているが，むしろ1面ずつ完成させず，代わりに交換子 $X,Y$ に即した方法は無いだろうか．3面体のみに限定すれば， $X^2,X^3$ などである程度の構成ができそうな手触り．まずは，そこを探ってもらうことに．
最後にweb上で様々な代数計算のできる，SageMathCellを紹介した．捗るかな．
sagecell.sagemath.org

群論の味わい－置換群で解き明かすルービックキューブと15パズル－

作者:David Joyner
共立出版

Amazon

2023-10-03

ライツアウトの数理（4年ゼミ）

ゼミ2023年度卒

ライツアウトの数理．
今回は，まず Jordan標準形について調べてきてもらった．
一通りその仕組を納得してもらった後， $\mathbb{F}_2$ で起こる現象について，少しずつ話すことにした．
例えば， $\mathbb{F}_2$ 係数の行列 $A=\begin{pmatrix}1&1\\1&1\end{pmatrix}$ の固有方程式は $\lambda^2=0$ となるから 0 が重複度2の固有値となる． $A$ は対称行列なのだが，固有ベクトルは $\begin{pmatrix}1\\1\end{pmatrix}$ の一つしかない．したがって，対角化もできない，といったことが起こる．実際，この場合 Jordan標準形は $\begin{pmatrix}0&1\\0&0\end{pmatrix}$ になる．

また，Jordan細胞のべき乗にも $\mathbb{F}_2$ ならではの現象が起こる．標数0の体では，固有値 $\lambda$ の $d$ 次元 Jordan細胞 $J(\lambda,d)$ のべき乗が
$J(\lambda,d)^n=\begin{pmatrix} \lambda^n & {n \choose 1}\lambda^{n-1} & {n\choose 2}\lambda^{n-2}& {n\choose 3}\lambda^{n-3}&\cdots\\ 0& \lambda^n & {n \choose 1}\lambda^{n-1} & {n\choose 2}\lambda^{n-2}& \cdots\\ 0&0& \lambda^n & {n \choose 1}\lambda^{n-1} & \cdots\\ 0&0&0& \lambda^n & \cdots\\ \end{pmatrix}$
となるが，これを $\mathbb{F}_2$ で考えると対角行列になることがある．実際 $n=2^b$ の場合，
$\displaystyle{n\choose k}=\frac{2^b}{k}\frac{2^b-1}{1}\frac{2^b-2}{2}\cdots\frac{2^b-k+1}{k-1}$
と変形すると， $s=2^e\cdot m, m:odd$ に対して $\frac{2^b-s}{s}=\frac{2^{b-e}-m}{m}$ と奇数/奇数の既約分数になるので， ${n\choose k}=\frac{2^b}{k}\cdot\frac{odd}{odd}$ と表され， $1\le k\le 2^b-1$ であれば ${n\choose k}\equiv0\pmod{2}$ ということになる．したがって， $2^b\ge d$ ならば $J(\lambda,d)^{2^b}=\lambda^{2^b}E_d$ となる．

こういった $\mathbb{F}_2$ 特有のできごとが，後々役立ってくる．

drive.google.com

2023-09-27

結晶群，キューブ群（４年ゼミ）

ゼミ2023年度卒

一人目，結晶群． $SO(3)$ の有限部分群の決定その２．
今日は2面体群～８面体群まで．残るは正２０面体群．

文様の幾何学―文様における群作用と対称性

作者:川崎徹郎
牧野書店

Amazon

二人目，キューブ群．オリジナルの手順を見つける話の続き．
よくやるよ，というぐらいの手順計算と実際の操作の試行錯誤．
もうちょっとで完成しそうではあったが，さて．

群論の味わい－置換群で解き明かすルービックキューブと15パズル－

作者:David Joyner
共立出版

Amazon

2023-09-26

ライツアウトの数理（4年ゼミ）

ゼミ2023年度卒

ライツアウトの数理も再開．
前期までは何とかして ${\rm rank}(M_n)$ が2項からなる場合だけでも解決できないかと悩んでいたが，この夏にあれこれ考えてみて，任意次数のライツアウトに対しての ${\rm rank}(M_n)$ が決定できることが分かった．そのポイントとなる仕組みが，Fibonacci多項式である．

ここでは $q_0(t)=p_{-1}(t)=0,q_1(t)=p_0(t)=1$ から始めて，
$\begin{pmatrix}p_{n+1}(t)\\q_{n+1}(t)\end{pmatrix}=\begin{pmatrix}t&1\\1&0\end{pmatrix}\begin{pmatrix}p_n(t)\\q_n(t)\end{pmatrix}$
によって定まる多項式をFibonacci多項式と呼ぶことにするが，一般にはこのうち $q_n(t)$ のほうを指す．すぐ分かるように， $q_{n+1}(t)=p_{n}(t)$ なので，漸化式

$p_{n+2}(t)=tp_{n+1}(t)+p_n(t)$

が得られる．この多項式を用いると，結論は

${\rm rank}(M_n)=n-\deg({\rm GCD}(p_n(t),p_n(t+1)))$

となるということだ．ここで ${\rm GCD}(f(t),g(t))$ は多項式 $f(t),g(t)$ の最大共通因子を表し， $\deg(f(t))$ は $f(t)$ の次数を表す．

これが正しそうか，幾つかの例で見てみよう．そのために，写像 $\sigma(n)=2n+1$ を用意しておく．これは，以下のようなFibonacci多項式の性質に由来する．
まず， $n\ge1$ に対して，
$\begin{pmatrix}t&1\\1&0\end{pmatrix}^n=\begin{pmatrix}p_{n}(t)&p_{n-1}(t)\\p_{n-1}(t)&p_{n-2}(t)\end{pmatrix}$
が帰納的に分かるので，等式
$\begin{align*} \begin{pmatrix}p_{m+n}(t)&p_{m+n-1}(t)\\p_{m+n-1}(t)&p_{m+n-2}(t)\end{pmatrix} &=\begin{pmatrix}t&1\\1&0\end{pmatrix}^{m+n}=\begin{pmatrix}t&1\\1&0\end{pmatrix}^m\begin{pmatrix}t&1\\1&0\end{pmatrix}^n\\ &=\begin{pmatrix}p_{m}(t)&p_{m-1}(t)\\p_{m-1}(t)&p_{m-2}(t)\end{pmatrix}\begin{pmatrix}p_{n}(t)&p_{n-1}(t)\\p_{n-1}(t)&p_{n-2}(t)\end{pmatrix} \end{align*}$
を通じて

$\begin{align*} p_{m+n}(t)&=p_m(t)p_n(t)+p_{m-1}(t)p_{n-1}(t)\\ p_{m+n-1}(t)&=p_{m-1}(t)p_{n}(t)+p_{m-2}(t)p_{n-1}(t) \end{align*}$

が得られる．さらに $m=n$ とすると，

$p_{2n-1}(t)=p_{n-1}(t)(p_n(t)+p_{n-2}(t))=tp_{n-1}(t)^2\text{ すなわち }p_{\sigma(n)}(t)=tp_n(t)^2$

が得られる．ただし， $\mathbb{F}_2$ での演算なので，Fibonacci多項式の漸化式が
$p_n(t)+p_{n-2}(t)=tp_{n-1}(t)$
とも表されることを使った．また以下では，しばしば
$(a+b)^{2^i}=a^{2^i}+b^{2^i}$
が成り立つことを使う．たとえば $p(t)^2=p(t^2)$ などと書き換えられる．

2021年度卒論で得られた結果の一つが， $n=2^m-1$ のとき ${\rm rank}(M_n)=n$ ということだった．一方， $2^{m+1}-1=\sigma^m(1)$ に気づけば，帰納的に

$p_1(t)=t,p_3(t)=p_{\sigma(1)}(t)=tp_1(t)^2=t^3,\dots,p_{\sigma^m(1)}(t)=t^{2^{m+1}-1}$

が分かる．すると， $g(t)={\rm GCD}(p_n(t),p_n(t+1))={\rm GCD}(t^n,(t+1)^n)=1$ となり， $\deg(g(t))=0$ なので， $n-\deg(g(t))=n$ で先程の結果に一致する．

また，卒論では $p_n(t)$ が2項からなる場合（ $n=3\cdot2^m-1$ ）について ${\rm rank}(M_n)=2^m+1$ と予想していた． $n=3\cdot2^m-1=\sigma^m(2)$ に気づけば，帰納的に

$\begin{gather*} p_2(t)=t^2+1=(t+1)^2,p_5(t)=p_{\sigma(2)}(t)=tp_2(t)^2=t(t+1)^4,\\ \dots,p_{\sigma^m(2)}(t)=t^{2^m-1}(t+1)^{2^{m+1}}\end{gather*}$

が得られる．さてすると， $2^m-1<2^{m+1}$ なので，

$\begin{align*} g(t)&={\rm GCD}(p_n(t),p_n(t+1))={\rm GCD}(t^{2^m-1}(t+1)^{2^{m+1}},(t+1)^{2^m-1}t^{2^{m+1}})\\ &=t^{2^m-1}(t+1)^{2^m-1} \end{align*}$

となるから， $\deg(g(t))=2(2^m-1)$ であり，

${\rm rank}(M_n)=3\cdot2^m-1-2(2^m-1)=2^m+1$

となって，卒論で予想したとおりの値となった．

タカラから発売された $5\times 5$ のオリジナルのライツアウトでは， $5^2=25$ -次元のライツアウト行列 $A$ を考えることになるが，そのランクが，
${\rm rank}(A)=5\cdot4+{\rm rank}(M_5)=20+(5-2)=23$
となり，よく知られた結果に一致する．つまり，あのゲームでは，2次元分の解の自由度があり，また，解がない（all offにできない）初期配置があるということだ．
drive.google.com

2023-09-20

結晶群，キューブ群（４年ゼミ）

ゼミ2023年度卒

ようやく，ゼミ再開．

一人目，キューブ群．
完成形に至る手順の考察．今回はツクダ式と呼ばれる揃え方について．
汎用的な手順を5つ用意し，あらゆるパターンをそれらの手順が使える配置に直すことで完成させる．
こういった方法，キューブ群のCayley graphで見ると何をしていることになるのだろう．
サイズ2のキューブで実験的に考えても良さそうだ．

群論の味わい－置換群で解き明かすルービックキューブと15パズル－

作者:David Joyner
共立出版

Amazon

二人目，結晶群．
ようやく，ようやく $SO(3)$ が登場．
これから， $SO(3)$ の有限部分群がこれまで出てきた群で尽くされることを示すようだ．
Burnside's Lemmaをうまく使って，場合を制限していくやりかた．なるほどね．

文様の幾何学―文様における群作用と対称性

作者:川崎徹郎
牧野書店

Amazon

2023-07-04

ライツアウトの数理（4年ゼミ）

ゼミ2023年度卒

ライツアウトの数理．
$T_n, n=3\cdot2^h-1$ と ${}^t(e)=(\delta_{i2^h}),{}^t(f)=(\delta_{i2^{h+1}})$ に対して，
$T_n^{2^{h+1}}e=T_n^{2^{h+1}}f\equiv 0\pmod{2}$
がようやく本日解決．
まず，境界の影響を受けずに $T_n^{2^h}e=T_n^{2^h}f=e+f$ まで示されるので，これを利用すれば
$T_n^{2^{h+1}}(e+f)=2(e+f)\equiv0\pmod{2}$
となるからだ．
その際，キーになるのが係数 $A^{2^{h}}_m$ に現れる ${}_{2^h}C_k$ の偶奇性だった．
実際， $k=2^pq, 0\leq p < h,q：奇数$ と表して
$\displaystyle {}_{2^h}C_k=\frac{2^h}{2^pq}\cdot\frac{2^h-1}{1}\cdot\frac{2^h-2}{2}\cdots\frac{2^h-k+1}{k-1}$
と書くと，冒頭 $\displaystyle \frac{2^h}{2^pq}=\frac{2^{h-p}}{q}$ からは2冪が残る可能性があり，それ以降は， $l=2^ij, 0 \leq i < h,j：奇数$ において，
$\displaystyle \frac{2^h-l}{l}=\frac{2^{h-i}-j}{j}$
となるから，分母分子に2冪は一つも現れなくなる．
したがって， ${}_{2^h}C_k$ が奇数となるのは $k=0$ または $p=h$ すなわち $k=2^h$ のときのみ，となった．

$A^t_m$ は $(1+x+x^2)^t$ の $x^m$ の係数を表していた．
この係数はまた，無限次の三重対角 $T_\infty$ と， $v$ 行目のみ1で他は0とした無限次のベクトル $e_v$ を考えたとき，ベクトル $T_\infty^te_v$ の $(v-t+m)$ 行目の成分でもある．
しかし実際の行列 $T_n$ においては，1行目から $n$ 行目のみでその前後は切り取られてしまうため，永続的に $A^t_m$ が正確な係数を表すわけではない．
そこで， $f_v$ を $e_v$ の1行目から $n$ 行目まで抜き出した $n$ 次元ベクトルとして， $T^t_nf_v$ が $T^t_\infty e_v$ の1行目から $n$ 行目に一致していることを
$T^t_nf_v\sqsubset T^t_\infty e_v$
と表そう．この関係はつまり， $A_0^t,\dots,A_{2t}^t$ すべてが境界での切り落としの影響を受けないことであり，
$1\le v-t+0\le v-t+2t\le n$ すなわち $t+1\le v\le n-t$
が条件となろう．
drive.google.com

2023-06-30

ピタゴラス数（４年ゼミ）

ゼミ2023年度卒

ピタゴラス数． $A^2+B^2-AB=C^2$ の整数解については，ほぼ見通しがたった．
そこで，このあとどう展開していくか，なのだが，例えば $X^2+Y^2=n$ に由来する整数解探しなどを提案した．
$n=3$ などでは有理点がないのでそもそも議論から外れるが， $n=2$ のときなど，まだまだ遊べそうな話題じゃないだろうか．